Neutrino Oscillations in the Sun
The neutrinos produced in the solar core experience decreasing matter density as they travel outward through the Sun. The neutrino propagation eigenstates are different from the flavor states in general 1. Because the density change inside the Sun is not dramatic, the flavor quantum states of the neutrinos will evolve adiabatically inside the Sun.
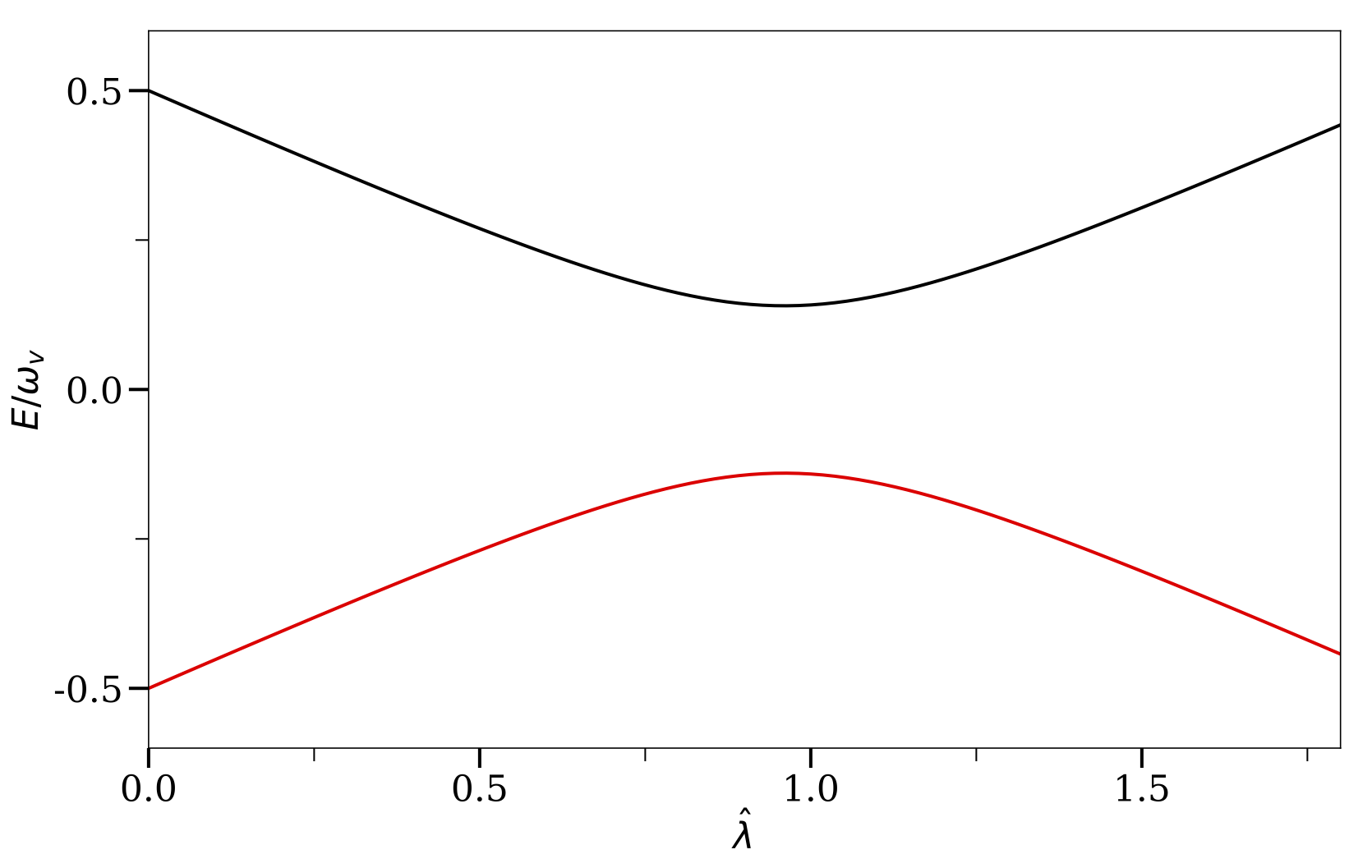
MSW Energy Levels
The two eigenvalues of the neutrino Hamiltonian as functions of matter potential $\hat\lambda$. I have used $\sin^2\theta_\vv = 0.02 \approx \sin^2 \theta_{13}$.
The values of the instantaneous eigenstates of the Hamiltonian, known as the “Heavy'' and “Light'' states, are $$ \begin{align} \varepsilon_{\mathrm H} &= \frac{\omega_\vv}{2}\sqrt{ \hat\lambda +1 - 2\hat\lambda \cos 2\theta_\vv }, \\ \varepsilon_{\mathrm L} &= -\frac{\omega_\vv}{2}\sqrt{ \hat\lambda +1 - 2\hat\lambda \cos 2\theta_\vv }, \end{align} $$ where $$ \begin{align} \hat\lambda & = \frac{\lambda}{\omega_\vv}. \end{align} $$ In Fig. MSW Energy Levels, I show the two eigenvalues of the neutrino Hamiltonian as functions of the matter potential $\hat \lambda$.
For a very high matter density, the heavy state of the neutrino $\ket{\nu_{\mathrm H}}$ is almost the same as $\ket{\nu_{\ee}}$. As the matter density decreases, $\ket{\nu_{\mathrm H}}$ becomes a mixture of different neutrino flavors. As the neutrino reaches the surface of the Sun, where the matter density is approximately zero, $\ket{\nu_{\mathrm H}}$ is about the same as vacuum mass eigenstate $\ket{\nu_{2}}$. As a result, the electron flavor neutrinos produced at the solar core are partially converted to other flavors as they reach the surface of the Sun. This explains the solar neutrino problem.
L. Wolfenstein, “Neutrino oscillations in matter”, Physical Review D 17, 2369-2374 (1978). ↩︎