Neutrino Oscillations in Matter
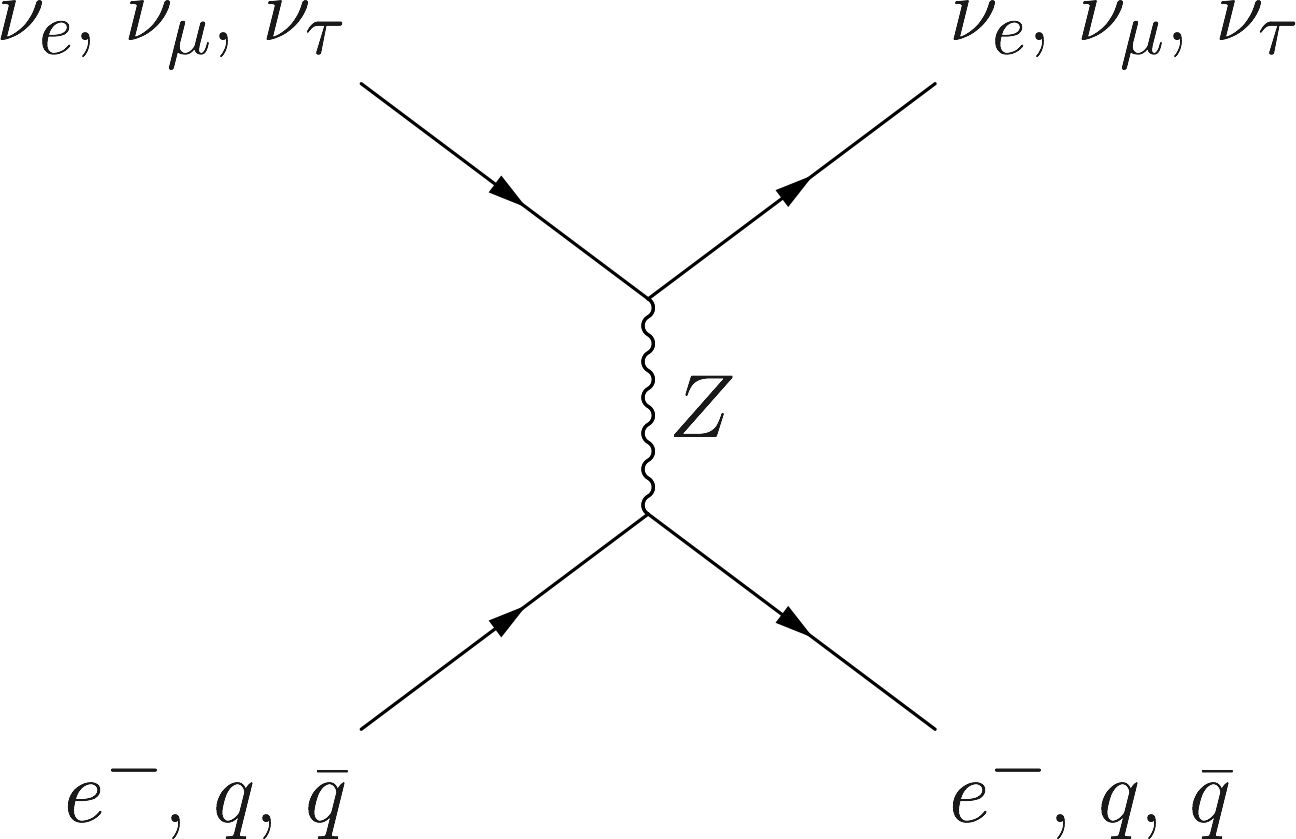
Neutral Current
The neutral current weak interaction does not distinguish between neutrino flavors and has no impact on neutrino oscillations.
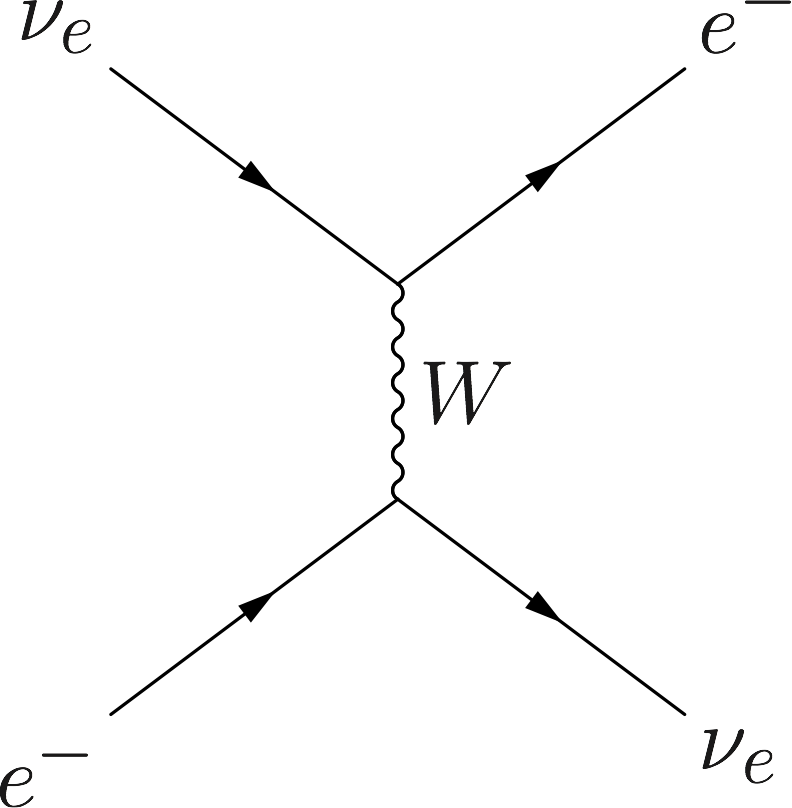
Charged Current
The electron flavor neutrino acquires a unique refractive index contribution from the charged current weak interaction with ambient electrons.
In many astrophysical environments such as stars and core-collapse supernovae, neutrinos are mostly produced at the center of the environments and propagate through the dense matter envelope. Although this matter envelope is essentially transparent to neutrinos, the refractive indices of the neutrinos in matter are different than those in the vacuum.1 Because the neutral current weak interaction does not distinguish between neutrino flavors (see Fig. Neutral Current), it has no impact on neutrino oscillations, and I will ignore it from now on. Meanwhile, the electrons and positrons in matter will cause electron flavor neutrinos to have refractive indices different than the neutrinos of other flavors through the charged current weak interaction (see Fig. Charged Current}).
This leads to an effective potential $$ \begin{equation} \mathsf V^{(\ff)} = \frac{\sqrt{2}G_{\mathrm F} n_{\mathrm e} }{2} \sigma_3, \label{chap:basics-sec:oscillations-matter-eqn:effective-pot} \end{equation} $$ where $G_{\mathrm F}=1.17\times 10^{-5}\mathrm{GeV^{-2}}$ is Fermi constant and $n_{\mathrm e}$ is net number density of the electron. As usual, I have ignored the trace terms in the above expression.
The Hamiltonian with the matter effect is the combination of Eqn. \eqref{chap:basics-sec:vacuum-osc-eqn:hamiltonian-vacuum} and Eqn. \eqref{chap:basics-sec:oscillations-matter-eqn:effective-pot}: $$ \begin{equation} \mathsf H^{(\ff)} = \left(\frac{\lambda}{2} -\frac{ \omega_\vv }{2} \cos 2\theta_\vv \right) {\sigma}_3 + \frac{ \omega_\vv }{2} \sin 2\theta_\vv {\sigma}_1, \label{chap:basics-sec:msw-eqn:hamiltonian-matter-effect} \end{equation} $$ where $$ \begin{equation} \lambda = \sqrt{2}G_{\mathrm F} n_{\mathrm e}. \label{chap:basics-sec:oscillations-matter-eqn:lambda} \end{equation} $$ Due to the off-diagonal terms in $\mathsf H^{(\ff)}$, the neutrino will experience oscillations in flavor. A resonance with the maximum flavor mixing occurs when the diagonal terms of $\mathsf H^{(\ff)}$ vanish, i.e., $$ \begin{equation} \frac{\lambda}{2} -\frac{ \omega }{2} \cos 2\theta_\vv = 0, \label{chap:basics-eqn:msw-resonance} \end{equation} $$ which gives the Mikheyev-Smirnov-Wolfenstein (MSW) resonance condition.
The word “matter” in this book refers to ordinary matter composed of electrons, positrons, nucleons and nuclei. I assume that the temperature and density of the environment are not high enough to produce muons and tau particles. I will discuss the effect of the dense neutrino medium in Chapter 4 Collective Neutrino Oscillations. ↩︎