Flavor Isospin Formalism
The Hamiltonian for two-flavor neutrino oscillations describes a two-level quantum system. It is known that two-level quantum systems can be visualized using the Bloch sphere. In the realm of neutrino physics, the neutrino flavor isospin was introduced for such purpose 1.
Illustration of Flavor Isospin
In the flavor isospin picture, a flavor isospin pointing upward, i.e., along the third axis in flavor space, indicates that the neutrino is in the electron flavor, while the downward direction indicates the other flavor, such as the muon flavor.
Every two-by-two Hermitian matrix can be expanded in the quaternion basis. For example, the Hamiltonian for neutrino oscillations in vacuum (in the flavor basis) can be written as $$ \begin{equation} \mathsf H^{(\ff)} = - \frac{\vec{\sigma} }{2}\cdot {\vec{H}}, \end{equation} $$ where $$ \begin{align} {\vec H} = \omega_\vv\begin{pmatrix} \sin \theta_\vv\\ 0\\ \cos 2\theta_{\mathrm v} \end{pmatrix}, \end{align} $$ which is a vector of length $\omega_{\mathrm v}$ and tilted away from the third axis by angle $2\theta_{\mathrm v}$. Throughout the book, I will use “$\vec{\phantom{x~}}$” to denote a vector in flavor space. The flavor quantum state of the neutrino is represented by its flavor isospin which is defined as $$ \begin{equation} \vec s = {\Psi^{(\ff)}}^{\dagger} \frac{\vec{\sigma} }{2} \Psi^{(\ff)}. \end{equation} $$ As shown in Fig. Illustration of Flavor Isospin, the direction of the flavor isospin in flavor space shows the flavor content of the neutrino. A flavor isospin pointing “upward'' in flavor space, i.e., along the direction of the third axis, denotes the electron flavor by definition. Correspondingly, the equation of motion for the flavor isospin describes its precession around the vector $\vec{H}$, $$ \begin{equation} \dot{\vec{s}} = {\vec{s}} \times \vec{H}, \label{chap:basics-sec:flavor-isospin-pic-eqn:eom-precession} \end{equation} $$ where $\dot{\phantom{s}}$ indicates the time derivative. In the flavor isospin formalism, the electron flavor survival probability is $$ \begin{equation} P = \frac{1}{2} + s_3, \label{chap:basics-sec:flavor-isospin-pic-eqn:probability-flavor} \end{equation} $$ where $s_3$ is the third component of the flavor isospin.
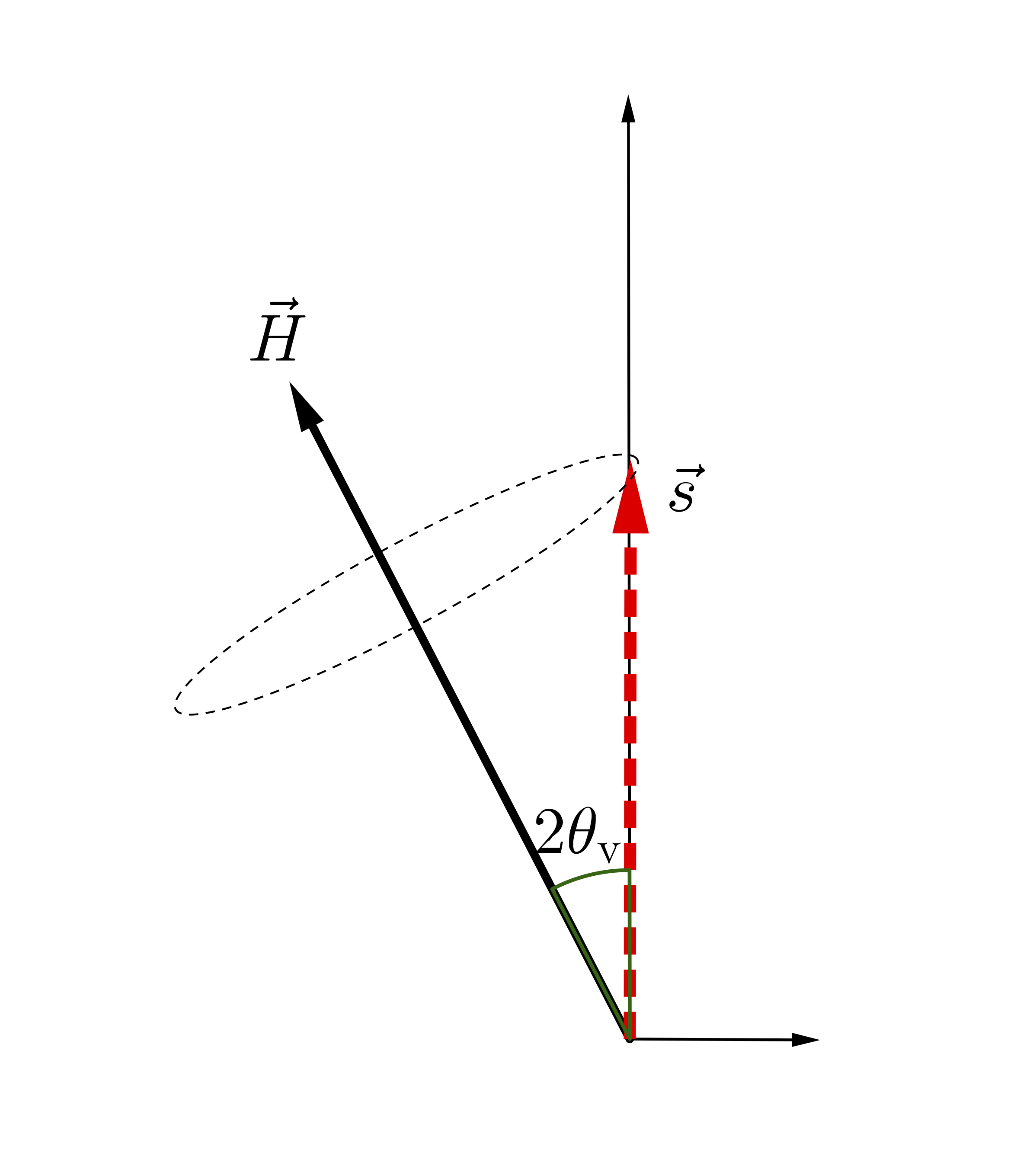
Flavor Isospin View of Vacuum Oscillations
Vacuum oscillations in the flavor isospin picture. The flavor isospin of a neutrino starting with the electron flavor precesses around the static “Hamiltonian vector” $vec H$, which gives a periodic flavor oscillation.
Therefore, the precession of the flavor isospin corresponds to a periodic oscillation between the two neutrino flavors (see Fig. Flavor Isospin View of Vacuum Oscillations). The oscillation frequency can be trivially read out from Eqn. \eqref{chap:basics-sec:flavor-isospin-pic-eqn:eom-precession}: $$ \begin{equation} \omega_\vv = \lvert \vec{H} \rvert. \end{equation} $$
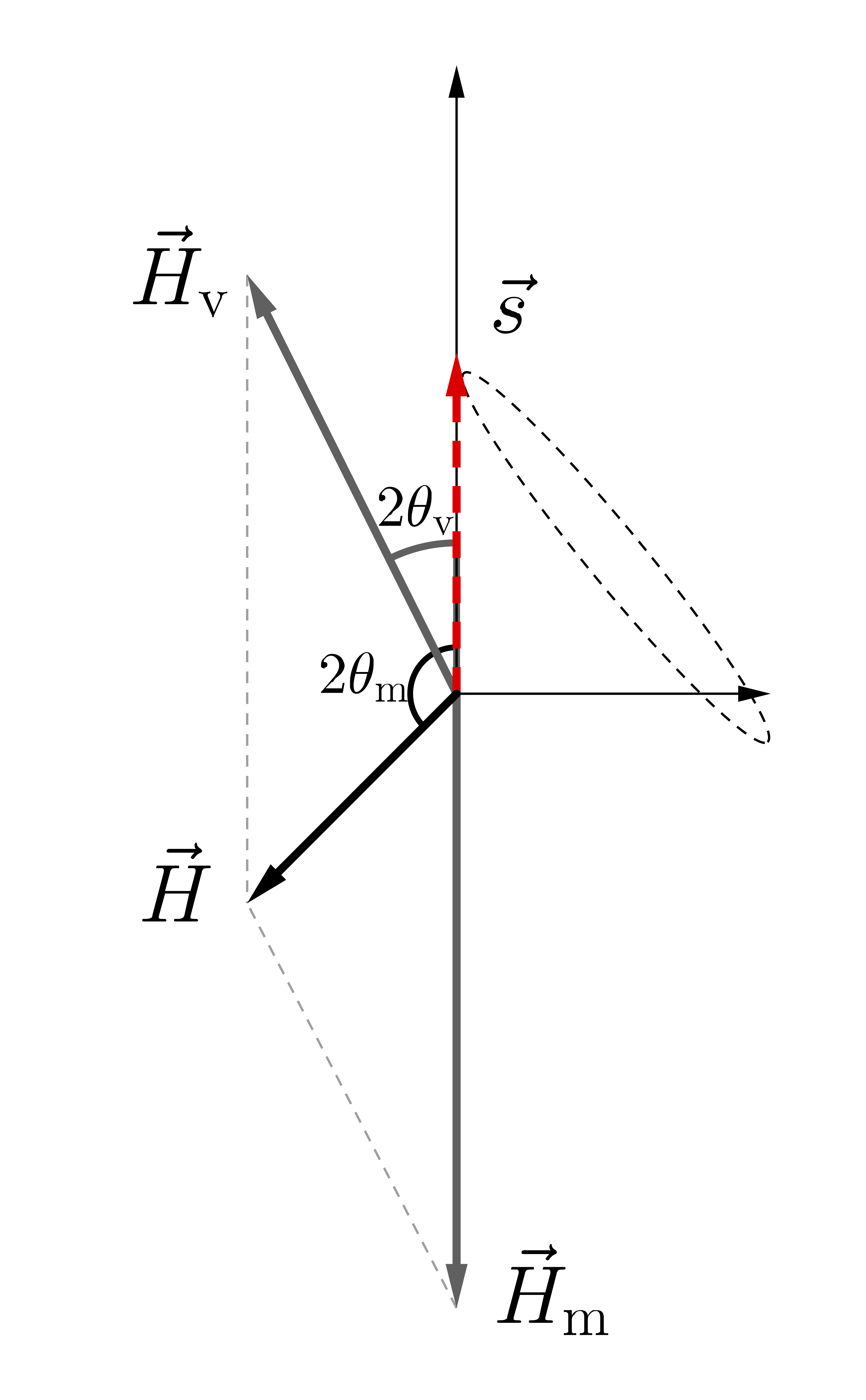
Oscillations in Not-so-large Matter Density
Neutrino oscillations in flavor isospin picture with the presence of matter potential. The flavor isospin is denoted as red-dashed arrow. The two gray vectors stand for the vacuum Hamiltonians $\vec H_{\mathrm v}$ and matter potential $\vec H_{\mathrm m}$.
The MSW effect can also be easily explained using the flavor isospin picture. The Hamiltonian for the neutrino flavor evolution in the presence of dense matter is $$ \begin{align} &\mathsf H^{(\ff)} = \frac{\omega_{\mathrm{v}}}{2}\left( - \cos 2\theta_{\mathrm{v}} {\sigma_3} + \sin 2\theta_{\mathrm{v}} {\sigma_1} \right) + \frac{\lambda(x)}{2} {\sigma_3} \\ \Rightarrow &\vec H = \vec H_{\mathrm v} + \vec H_{\mathrm m}(x) = \omega_{\mathrm v}\begin{pmatrix} - \sin 2\theta_{\mathrm v} \\ 0 \\ \cos 2\theta_{\mathrm v} \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ - \lambda(x) \end{pmatrix} , \end{align} $$ where $\vec H_{\mathrm v}$ is the vacuum Hamiltonian, and $\vec H_{\mathrm m}(x)$ is the matter potential. The precession motion of the flavor isospin of the neutrino in the presence of dense matter is visualized in Fig. Oscillations in Not-so-large Matter Density. The MSW resonance condition in Eqn. \eqref{chap:basics-eqn:msw-resonance} corresponds to the scenario that the overall “Hamiltonian vector” $\vec H$ is perpendicular to the third axis in flavor space. In this case, the flavor isospin rotates in the plane spanned by the second and third axes which give maximum flavor oscillations (see Fig. Oscillations in Critical Matter Density).
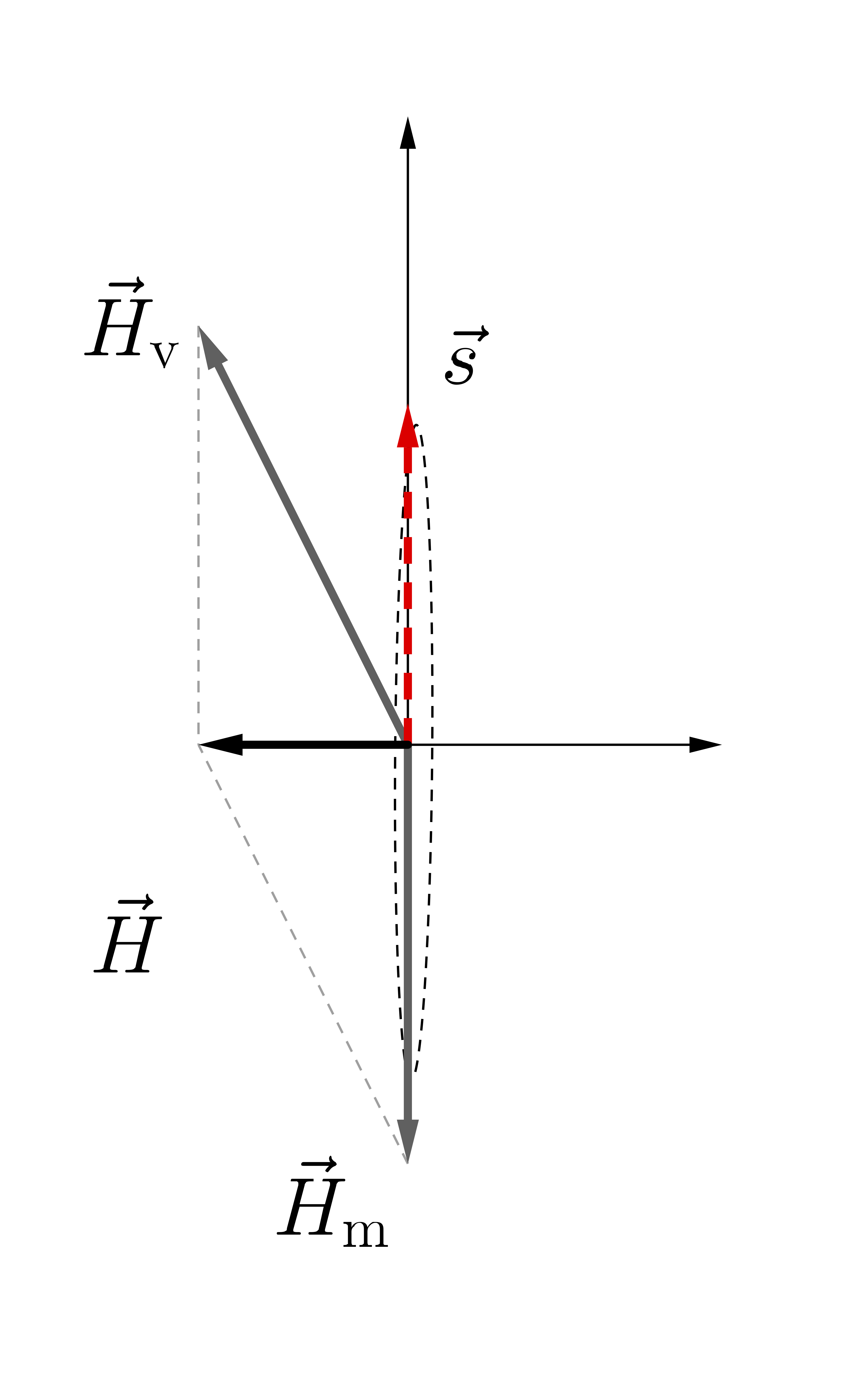
Oscillations in Critical Matter Density
MSW resonance occurs when resonance condition is satisfied.
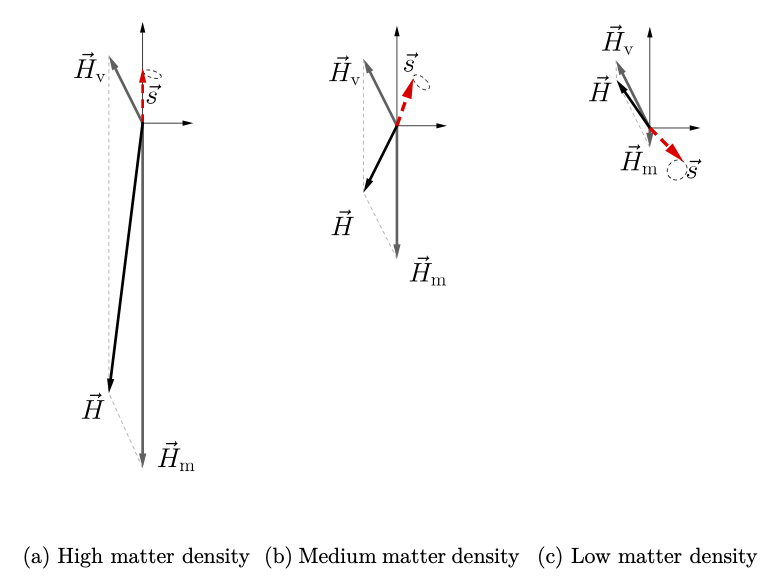
The adiabatic flavor evolution of the neutrino in a varying matter density profile discussed in Sec.~\ref{chap:matter-sec:solar-neutrinos} can also be easily understood in the flavor-isospin picture. In the region where the matter density is high, the total “Hamiltonian vector” $\vec H$ points “downward'' in flavor space. Therefore, a neutrino produced in the electron flavor will experience very little oscillation because its flavor isospin $\vec s$ is almost anti-parallel to $\vec H$ (see Fig. MSW Adiabatic). If the matter density along the propagation trajectory of the neutrino decreases slowly, $\vec s$ will stay almost anti-parallel to $\vec H$ as $\vec H$ rotates (see Fig. MSW Adiabatic). When the neutrino reaches the region with very low matter density, its flavor isospin becomes almost anti-parallel to $\vec H_{\vv}$, which implies that the neutrino is in $\ket{\nu_2}$ (see Fig. MSW Adiabatic).
Oscillations in Critical Matter Density
Flavor isospin picture of neutrino oscillations in matter. $\vec H_{\mathrm v}$ is the vacuum Hamiltonian, and $\vec H_{\mathrm m}$ is the matter potential.
H. Duan, G. M. Fuller, and Y.-Z. Qian, “Analysis of collective neutrino flavor transformation in supernovae”, Physical Review D 74, 123004 (2006), arXiv:0703776[astro-ph]. ↩︎