Neutrino Oscillations with Reflected Fluxes
Most of the researches on supernova neutrino oscillations assumed that neutrinos are emitted from the spherical surface of a neutron star and that they are free streaming. In the real supernova environment, however, a small amount of neutrinos can be scattered back towards the neutron star. J. Cherry et al. showed that the “neutrino halo” formed by the scattered neutrino fluxes can change the neutrino self-interaction potential dramatically which may have an impact on neutrino oscillations in the supernova 1. In the section, I describe a toy model which can be used to explore the effect of the scattered neutrino fluxes on neutrino oscillations.
Two-Beam Model with Reflection
I will consider the two-beam model depicted in Fig. Two-Beam Line Model but with a “neutrino mirror” at $z=L$ that partially reflects the neutrino beams backward without changing their flavor content. The equations of motion for neutrino oscillations in this model are $$ \begin{align} \ri \sin\theta_i \partial_z \rho_i = & [ \mathsf H_i, \rho_i ] \qquad (i=1,2,3,4) \end{align} $$ where beams 1 and 2 contain neutrinos and antineutrinos, beams 3 and 4 are the reflected fluxes of 1 and 2, respectively, with $\theta_3=\theta_1$ and $\theta_4=\theta_2$. The Hamiltonians in the vacuum mass basis are $$ \begin{align} \mathsf H_1 =& -\eta \omega_\vv \sigma_3 + \mu( -\alpha \chi_- \rho_2 - \alpha \chi_+ R \rho_4 + \chi_1 R \rho_3), \\ \mathsf H_2 =& \eta \omega_\vv \sigma_3 + \mu( \chi_- \rho_1 -\alpha \chi_2 R \rho_4 + \chi_+ R \rho_3), \\ \mathsf H_3 =& -\eta \omega_\vv \sigma_3 + \mu( -\alpha R \chi_- \rho_4 -\alpha \chi_+ \rho_2 + \chi_1 \rho_1), \\ \mathsf H_4 =& \eta \omega_\vv \sigma_3 + \mu( R \chi_- \rho_3 + \chi_+ \rho_1 -\alpha \chi_2 \rho_2), \end{align} $$ where $\mu=\sqrt{2}G_{\mathrm F}n_1$ with $n_1$ being the number flux of beam 1, $\alpha=n_2/n_1$, $R$ is the reflection coefficient of the “neutrino mirror”, and $$ \begin{align} \chi_+ = & 1 - \cos ( \theta_1 + \theta_2 ), \\ \chi_- = & 1 - \cos ( \theta_1 - \theta_2 ), \\ \chi_1 = & 1 - \cos ( 2\theta_1 ), \\ \chi_2 = & 1 - \cos ( 2\theta_2 ). \end{align} $$
Relaxation Method
I developed a relaxation method to solve the two-beam model with reflection numerically. For the purpose of illustrating the algorithm, I denote the Hamiltonian using its components in flavor space: $$ \begin{equation} \mathsf H = -\sum_i \frac{H_i}{2}\sigma_i. \end{equation} $$ At position $z$, the evolution operator $\mathsf U(\Delta l,z)$ is $$ \begin{align} U(\Delta l, z) = \cos \left( \frac{H \Delta l}{2} \right) \mathsf I + \ri \left( \frac{H_1}{H} \sigma_1 + \frac{H_2}{H} \sigma_2 + \frac{H_3}{H} \sigma_3 \right) \sin \left( \frac{H \Delta l}{2} \right) \end{align} $$ where $\Delta l$ is the propagation distance along the neutrino trajectory between $z$ and the new position $z'$, and $$ \begin{equation} H = \sqrt{ H_1^2 + H_2^2 + H_3^2 }. \end{equation} $$ Then I calculate the density matrix at $z'$ as $$ \begin{align} \rho ( z' ) &= \mathscr F ( \mathsf H(z), \rho(z), \Delta l ) \\ &= \mathsf U (\Delta l, z) \rho(z)U^\dagger (\Delta l, z) \\ & = \frac{1}{4} \sum_j \left[ \cos( H \Delta l) \rho_j - \frac{2}{H^2} \sin^2 \left( \frac{H \Delta l}{2} \right) \sum_i H_i \rho_i H_j \right] \sigma_j. \end{align} $$ I discretize the $z$ axis into $N$ bins with $\Delta z = L/N$ and $z_n=n \Delta z$ ($n=0,1,\cdots, N$). I use the evolution operator $U_a(\Delta l, z)$ and the following iteration algorithm until I achieve numerical convergence.
| |
To speed up the calculations, I have parallelized the above algorithm with OpenMP.
Validation of the Relaxation Method with Relected Single-Neutrino-Beam
As a check to the relaxation algorithm discussed in the previous subsection, I apply it to the single-beam model with reflection, i.e., $\theta_1=\pi/2$ and $\alpha=0$. As the first step of the validation of the numerical code, I compare the numerical and analytical results for the vacuum oscillations case with $R\to 0$ and the normal neutrino mass hierarchy. The results are shown in Fig. Validation Model.
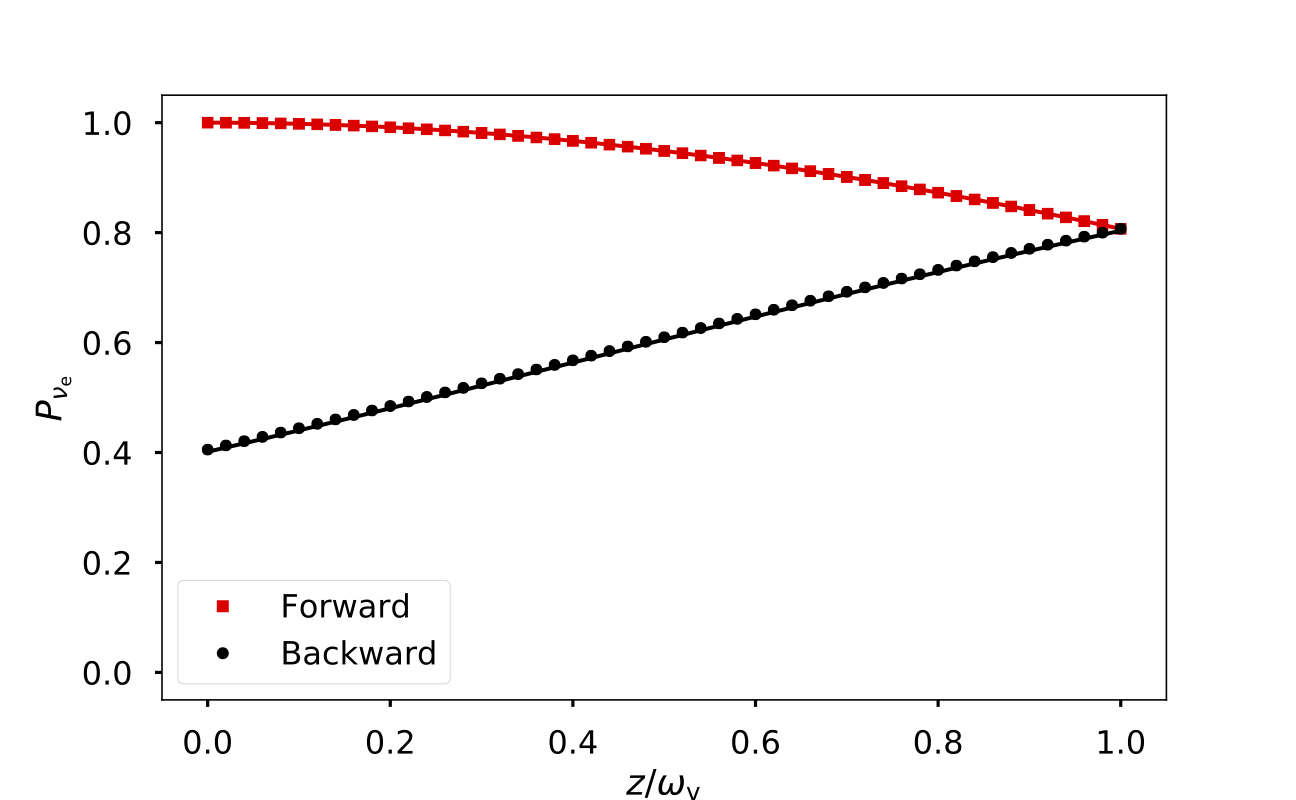
Validation Model
The validation of the numerical code for the single-beam model with $R\to 0$ and $L=1/\omega_\vv$. The markers and the continuous curves represent the numerical and analytical results, respectively.
To further validate the numerical code, I apply the linearized flavor stability analysis to the single-beam model with $R>0$ and compare it with the numerical results. The equation of motion in the linearized regime is $$ \begin{align} i\partial_z \begin{pmatrix} \epsilon_{\mathrm F} \\ \epsilon_{\mathrm B} \end{pmatrix} = \begin{pmatrix} -\eta\omega_\vv + R \mu' & - R \mu' \\ \mu' & \eta\omega_\vv - \mu' \end{pmatrix} \begin{pmatrix} \epsilon_{\mathrm F} \\ \epsilon_{\mathrm B} \end{pmatrix}, \label{chap:collective-sec:halo-eqn:linearized-eom-single-beam-model} \end{align} $$ where $\mu' = 2\mu$, and $\epsilon_\FF$ and $\epsilon_\BB$ are the off-diagonal elements of $\rho_1$ and $\rho_3$, respectively. This equation can be easily solved. The neutrino gas has two collective modes with oscillation frequencies $$ \begin{align} \Omega_\pm &= \frac{1}{2} [ (R-1)\mu' \pm \sqrt{\Delta} ], \end{align} $$ where $$ \begin{equation} \Delta = (1-R)^2 \mu'^2 - 4\mu' \eta\omega_\vv (1+R) + 4\omega_\vv^2. \end{equation} $$ The corresponding eigenvectors are $$ \begin{align} V_\pm &= \frac{1}{2\mu'}\begin{pmatrix} { -2\eta\omega_\vv + \mu' (1+R) \pm \sqrt{\Delta} } \\ 2\mu' \end{pmatrix}. \end{align} $$ The general solution to the equation of motion is $$ \begin{equation} \begin{pmatrix} \epsilon_{\mathrm F}(z) \\ \epsilon_{\mathrm B}(z) \end{pmatrix} = C_+ V_+ e^{-i \Omega_+ z} + C_- V_- e^{-i \Omega_- z}, \label{chap:collective-sec:halo-eqn:linear-solution-general-solution} \end{equation} $$ where $C_\pm$ are constants. Using the fact that $\epsilon_F(L)=\epsilon_B(L)$ at the “neutrino mirror”, I obtain $$ \begin{equation} \frac{C_+}{C_-} = e^{-i(\Omega_- -\Omega_+)L} \frac{ \sqrt{\Delta} + 2\eta\omega_\vv + \mu' \ (1-R) }{\sqrt{\Delta} - 2\eta\omega_\vv - \mu' (1-R)}. \label{chap:collective-sec:halo-eqn:linear-solution-general-solution-cp-cm-relations} \end{equation} $$ Combining Eqn.~\eqref{chap:collective-sec:halo-eqn:linear-solution-general-solution} and Eqn.~\eqref{chap:collective-sec:halo-eqn:linear-solution-general-solution-cp-cm-relations} I obtain $$ \begin{equation} \begin{pmatrix} \epsilon_{\mathrm F}(z) \\ \epsilon_{\mathrm B}(z) \end{pmatrix} = C_- e^{-i\Omega_- L} \left( \frac{ \sqrt{\Delta} + 2\eta\omega_\vv + \mu' (1-R) }{\sqrt{\Delta} - 2\eta\omega_\vv - \mu' (1-R)} V_+ e^{-i \Omega_+ (z-L)} + V_- e^{-i \Omega_- (z-L)} \right). \end{equation} $$
Since $\Delta < 0$ when there exist flavor instabilities in the neutrino gas, I define $i\delta = \sqrt{\Delta}$. Therefore, $$ \begin{align} \left\vert \epsilon_{\mathrm F} \right\vert \propto & \lvert (2\eta\omega_\vv + \mu'(1-R) +i \delta ) ( -2\eta\omega_\vv + \mu'(1+R) + i \delta ) e^{\delta(z-L)} \nonumber\\ &+ ( -2\eta\omega_\vv - \mu'(1-R) +i \delta ) ( -2\eta\omega_\vv + \mu'(1+R) - i \delta ) e^{-\delta(z-L)} \rvert, \label{chap:collective-sec:halo-eqn:linearized-eom-solution} \end{align} $$ which can be simplified as $$ \begin{equation} \left\vert \epsilon_{\mathrm F} \right\vert \propto A + B \cosh( 2\delta(L-z) ) \label{chap:collective-sec:halo-eqn:single-beam-linearized-solution} \end{equation} $$ with $$ \begin{align} A &= 8 \mu'^2 (\mu' - R - 2 \eta\omega_\vv )^2 + 8 \mu'^2 \Delta, \\ B &= 8 \mu'^2 (\mu' - R - 2 \eta\omega_\vv )^2 - 8 \mu'^2 \Delta . \end{align} $$ The only $z$ dependent term in Eqn.~\eqref{chap:collective-sec:halo-eqn:single-beam-linearized-solution} is $\cosh( 2\delta(L-z) )$, which decreases within $[0,L]$. In addition, $$ \begin{equation} \left. \frac{\dd \epsilon_\FF}{\dd z} \right \vert_{z=L} = \left. \frac{\dd \epsilon_\BB}{\dd z} \right \vert_{z=L} = 0. \end{equation} $$
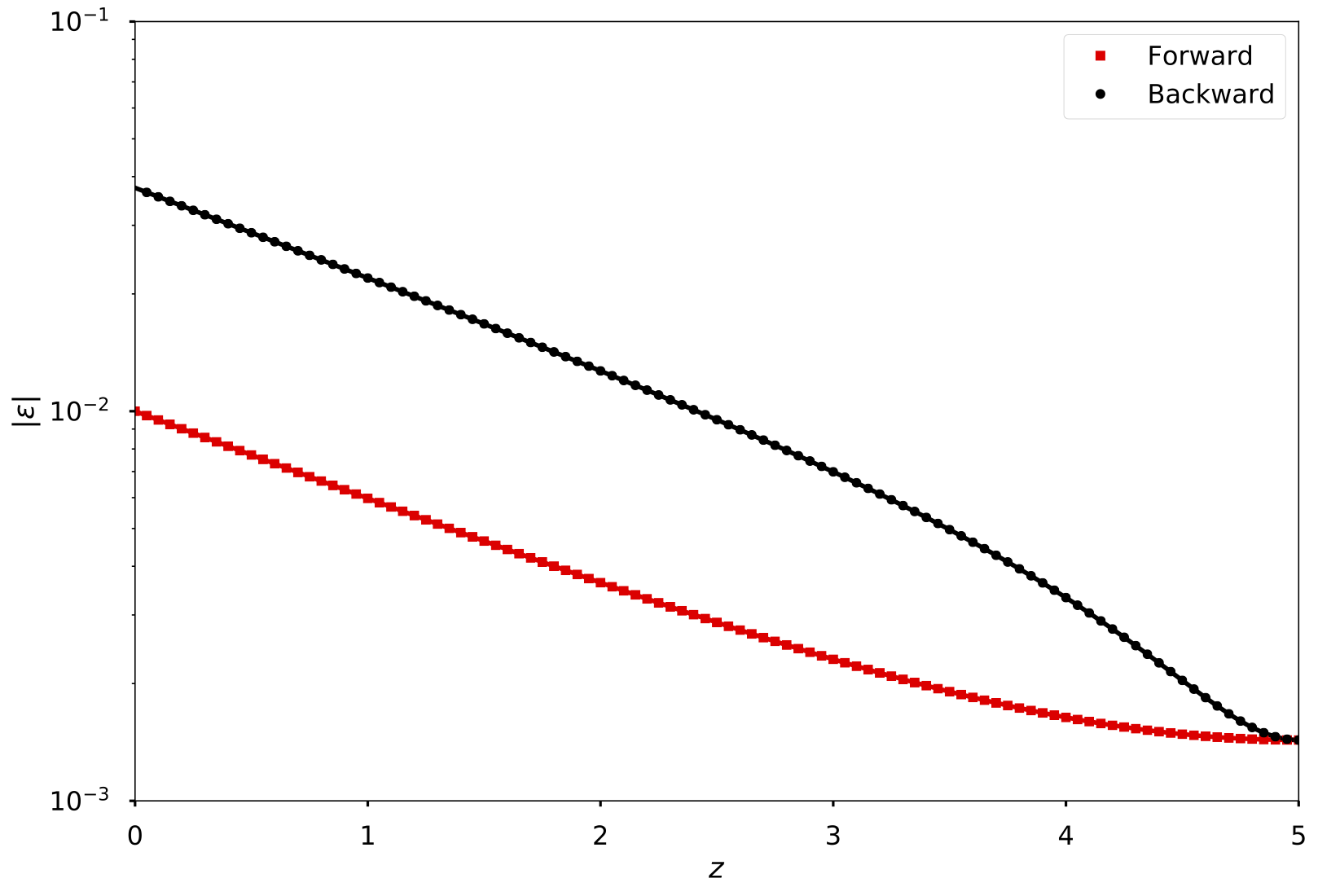
Magnitudes of the Off-diagonal Elements
The magnitudes of the off-diagonal elements of the density matrices of the forward and reflected neutrino beams as functions of distance $z$, respectively. The markers are the numerical results for the single-beam model with $\mu'= 1.0$, $R=0.07$, $L=5/\omega_\vv$, and the normal hierarchy. The continuous curves are the analytical results obtained from Eqn.~\eqref{chap:collective-sec:halo-eqn:linearized-eom-solution}.
For small values of $\epsilon_{\FF}$ and $\epsilon_\BB$, the solution from the linearized equation should represent the numerical calculations faithfully. In Fig. Magnitudes of the Off-diagonal Elements, I plotted the numerical result (dots) as well as the result from Eqn.~\eqref{chap:collective-sec:halo-eqn:single-beam-linearized-solution} (lines). It clearly shows that the linearized solution is a great match to the numerical result. This is also a method to validate the code.
In Fig. Magnitudes of the Off-diagonal Elements, I compare the numerical results obtained from the relaxation algorithm with the analytical results in Eqn.~\eqref{chap:collective-sec:halo-eqn:linearized-eom-solution} for the single-beam model with $\mu'= 1.0$, $R=0.07$, $L=5/\omega_\vv$, and the normal hierarchy. The good agreement between these results shows that the numerical code works as expected.
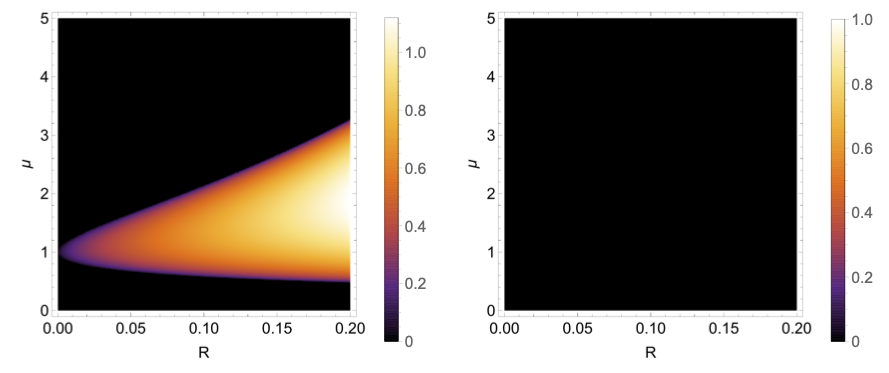
Instability Regions
Instability regions for the normal hierarchy (left) and the inverted hierarchy (right) in the single-beam model with reflection. The color represents the magnitude of the imaginary component of the collective frequency.
Comparing Eqn.~\eqref{chap:collective-sec:bipolar-linearized-eom} and Eqn.~\eqref{chap:collective-sec:halo-eqn:linearized-eom-single-beam-model}, one sees that the single-beam model with reflection is equivalent to the two-beam model without reflection except that the reflected neutrino beam now plays the role of the antineutrino, $R\to \alpha$, $\eta \to -\eta$, and $\mu' \to \mu$. Therefore, flavor instabilities should exist for the normal mass hierarchy in the single-beam-model with reflection (see Fig. Instability Regions).
John F. Cherry, "Neutrino scattering and flavor transformation in supernovae", Physical Review Letters 108, 1-5 (2012) . ↩︎